내가 보려고 만든 블로그
<Bayesian> MAB 톰슨 샘플링 본문
MAB ( Multi Armed Bandit) :
활용되는 곳이 많지만 주로 상품 , 광고추천등에서 어떤 것 을 사용자에게 보여주어야 이득이 최대가 될까?
동시에 특정 상품에 편향되지 않게 다양한 상품이 노출되게 할 수 있을까?
를 해결하는데 사용된다.
Epsilon- greedy, UCB등의 방법이 있는데 그 중에서도 많이 사용되는 Tomson Sampling 방법에 대해서 소개하고
Pyro를 이용해서 구현해봄.
베타분포

먼저 베타분포에 대해서 알아야 하는데 베타분포는 성공횟수 a-1 , 실패횟수 B-1 만큼 관측 되었을 때 성공확률에 대한 확률분포이다.
예를 들어 , a=1 , B=1 일 경우 사건이 발생하지 않은 경우이므로 성공확률은 어떤 정보도 없으므로 uniform distribution 형태가 될 것 이다. a=3 , B=3 일 경우 성공확률은 0.5 에서 가장 높고 대칭인 형태의 분포의가 나오게 된다.
Tomson Sampling
톰슨샘플링을 상품 추천에 대해 적용해서 설명해보고 구현도 해보았다. 사실 매우 간단해서 구현이라고 할 것도 없음.
우선 톰슨샘플링은 각 상품에 대해 베타분포를 가정한다.
클릭률이 각각 3% , 5% , 10% 인 경우의 베타분포 a,b,c 를 가정하였음.
import numpy as np
from scipy.special import beta
import matplotlib.pyplot as plt
import torch
beta_a = [3,100] # 3 %
beta_b = [6,120] # 5%
beta_c = [4,40] # 10 %
beta_distributions = np.array([beta_a,beta_b,beta_c])
x = np.linspace(0, 1)
f,ax = plt.subplots(1,1,figsize=(20,8))
for b in beta_distributions:
success = b[0]
fail = b[1] - b[0]
y = (1 / beta(success, fail)) * x ** (success - 1) * (1 - x) ** (fail - 1)
plt.plot(x,y)
다음으로 매 iteration 마다 3개의 베타분포에서 각각 샘플링을 한 후 가장 클릭률( x)이 높은 상품을 노출해주면 된다 .
지금 각각의 분포 a,b,c에서 샘플링을 한다면 좀더 오른쪽으로 치워치진 c > b > a 순으로 더 높은 x값을 기대해 볼 수 있다. ( exploit)
하지만 항상 그런것은 아니다! 낮은 확률이지만 a의 샘플링 결과가 다른 두 분포보다 크게 나올 확률도 여전히 존재한다. (explore)
샘플링을 한 결과 높은 값을 보여주고 베타분포를 매번 혹은 원하는 배치기간 마다 (ex - 매 10번 iteration 등) 업데이트 해주면 되겠다.
예시로는 샘플링을 한 결과를 항상 유저가 클릭했다고 가정하고 업데이트를 해보았다. ( 이런 경우는 없겠지만.. )
count = 0
beta_distribution_a = torch.distributions.Beta(beta_a[0],beta_a[1] - beta_a[0] )
beta_distribution_b = torch.distributions.Beta(beta_b[0],beta_b[1] - beta_b[0])
beta_distribution_c = torch.distributions.Beta(beta_c[0],beta_c[1] - beta_c[0])
beta_distributions
for i in range(1000):
samples = [beta_distribution_a.sample(), beta_distribution_b.sample() , beta_distribution_c.sample()]
click = np.argmax(samples)
beta_distributions[click][0] += 1
beta_distributions[:,1] +=11000번의 iteration 후 다음과 같이 1. 각 분포의 성공횟수, 전체횟수 2. 클릭률 이 변화하였다.
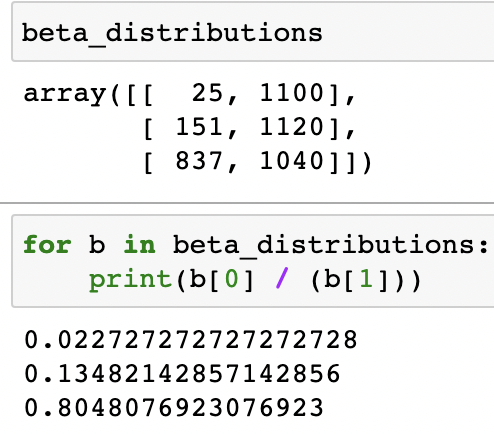
f,ax = plt.subplots(1,1,figsize=(20,8))
for b in beta_distributions:
success = b[0]
fail = b[1] - b[0]
y = (1 / beta(success, fail)) * x ** (success - 1) * (1 - x) ** (fail - 1)
plt.plot(x,y)
'Data Science > Bayesian' 카테고리의 다른 글
| <Bayesian> Bayesian Optimization (0) | 2022.11.27 |
|---|---|
| <Bayesian> Variational Inference ( Pyro) (0) | 2022.11.12 |
| <Bayesian> MCMC, pyro 로 모델링 (HMC) (0) | 2022.10.30 |
| <Bayesian> Bayesian Regression + Pyro 간단 정리. (0) | 2022.10.01 |



