내가 보려고 만든 블로그
<Bayesian> Bayesian Optimization 본문
Bayesian Optimization 을 이용하면 적은 시행만으로도 쉽게 Hyper Parameter 튜닝을 할 수 있다.
는 말을 ML 공부하는 사람이라면 한번 쯤은 들어봤을 듯.
어떻게 Bayesian Optimization이 몇번의 시행만으로 Hyper Parameter를 쉽게 튜닝할 수 있을까?? 에 대해서 간단하게 적어보았다.
Gaussian Process (GP)
우선 Gaussian Process (GP)에 대해서 공부해야 한다. Bayesian Optimizaition을 수행함에 있어 GP 방법만이 있는 것은 아니다. 하지만 GP가 가장 많이 사용되는 방법임.
Gausisian Process는 다변량 정규분포를 무한 차원으로 확장시킨 개념이다. 사실 "무한" 이라는 특징보다 Bayesian Optimizaition 을 이해함에 있어 중요한 특징은 따로 있다. 베이지안 리그레션의 경우 각 관측치 or 설명변수들이 서로 독립이다는 가정이 있는 것과 다르게 가우시안 프로세스의 경우에는 각 x_i 에서의 정규분포들 사이에 상관성을 가지고 있다. 회귀분석을 배울때 각 설명변수 x_i 에서 y의 값을 정규분포를 가정하는 것을 봤을 것이다. 이 정규분포들이 회귀분석 or 베이지안 리그레션등에서는 서로 독립이지만 가우시안 프로세스에서는 각 정규분포끼리 독립을 가정하지 않는다.
(일반적으로) 정규분포들끼리 연관이 되어있다 -> 공분산행렬 을 쉽게 떠올릴 수 있을 것이다. 살짝 다른 점은 공분산행렬 대신 커널함수를 사용하여 정규분포들끼리의 상관성을 나타낸다 . Kernel 함수의 경우에도 여러개가 있지만 대표적으로 많이 쓰이는 커널 함수에는 RBF 커널이 있다. ( 식에서 d = x_i와 x_j 의 유클리안 거리를 의미 )
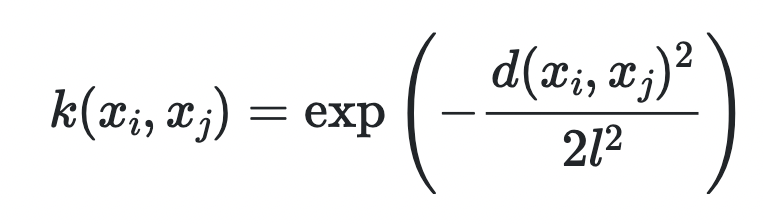
커널함수는 GP를 통해 모델을 학습할 때 사용되는데 관측치 ( 알고 있는 x_i) 와 가까울 경우 신뢰구간이 매우 좁아지고 멀 경우 신뢰구간이 점점 멀어지게 된다. 이 2가지 포인트 1. (베이지안 이므로) 점 추정이 아니라 확률분포로써 신뢰구간을 가짐. 2. 관측치와 가까운 지점은 신뢰구간이 매우 좁아지고 멀어질수록 신뢰구간이 커짐 ( 예를 들어 , f(100)을 추정함에 있어서 f(99)값이 f(1)값 보다 도움이 될 것 이라고 생각하는 것은 당연하다 . ) 를 바탕으로 다음 베이지안 옵티마이제이션을 이어서 설명하겠다.
추가로 , 커널 함수가 𝐾(𝑥𝑖,𝑥𝑗)=𝑥𝑖𝑥𝑗 라면 ( 즉, 서로 독립이라면) Bayesian Regression과 같은 문제가 된다.
1.일반적인 Regression 2. Bayesian Regression 3. Gaussian Process 의경우 다음과 같이 모델이 만들어지게 된다 .
Bayesian Optimization
이제 Bayesian Optimization이 어떻게 동작하는지 알아보자 . 먼저 추정하고자 하는 함수를 임의로 다음과 같이 정의 하였다.
x는 크기가 2인 list이고 2개의 값 x[0] 과 x[1]을 바탕으로 obj_func의 값이 나오게 된다.
def obj_func(x): # [a,b]
return x[0] ** 2 * np.sin(5* np.pi * (-x[0] + 2 * x[1]))그리고 샘플링을 수행하는 함수를 다음과 같이 정의 하였다.
import numpy as np
def sampler(n):
return np.random.random((n,2))먼저 샘플링(10개) 을 통해 최적화 하고 싶은 함수 obj_func에 대한 값을 관측해 준다.
그리고 샘플들(x)과 func(x)= Y 를 구함 .
X = sampler(n)
y = np.apply_along_axis(obj_func , axis = 1 , arr = X)X, y에 fit하는 가우시안 프로세스 모델을 만들어준다 . RBF 커널을 사용하였고 WhiteKernel은 노이즈 .
from sklearn.gaussian_process import GaussianProcessRegressor as GRR
from sklearn.gaussian_process.kernels import RBF , WhiteKernel
model = GRR(kernel = RBF() + WhiteKernel() , random_state =2022).fit(X,y)
10개의 샘플링을 통해 가우시안 프로세스 모델을 만들었다면 다음으로 어디를 탐색해야 할지를 정해야 하는데 이 척도로 acquisition function을 사용한다. 가장 많이 사용되는 방법은 EI (Expected Improvement) 이다. 강화학습에서 기본적인 idea가 되는 Exploration 과 Exploitation 방법을 적용하여 탐색을 해가는 방법이라는데 요약하자면 기존에 구한 best_mu (최고의 평균값) 보다 더 높은 값이 나올 확률을 새로 구한 x들 에 대해서 구하고 ( 그림에서 초록 부분 ) 그 확률이 가장 높은 x를 다음 탐색 지점으로 정하는 것이다. 수식이 다음과 같이 나온다고 한다. 근데 (mu-best_mu -e) * norm.cdf(z) 여기까지가 초록 부분의 영역인데 다음 항은 왜 더해주는지는 아직 모르겠다..
from scipy.stats import norm
def EI(X_new, model , best_mu , e= 0.01):
mu , sigma = model. predict(X_new , return_std = True)
z= np.zeros(len(X_new))
z[sigma>0] = ((mu- best_mu -e ) / sigma )[sigma>0]
return (mu-best_mu -e) * norm.cdf(z) + sigma * norm.pdf(z)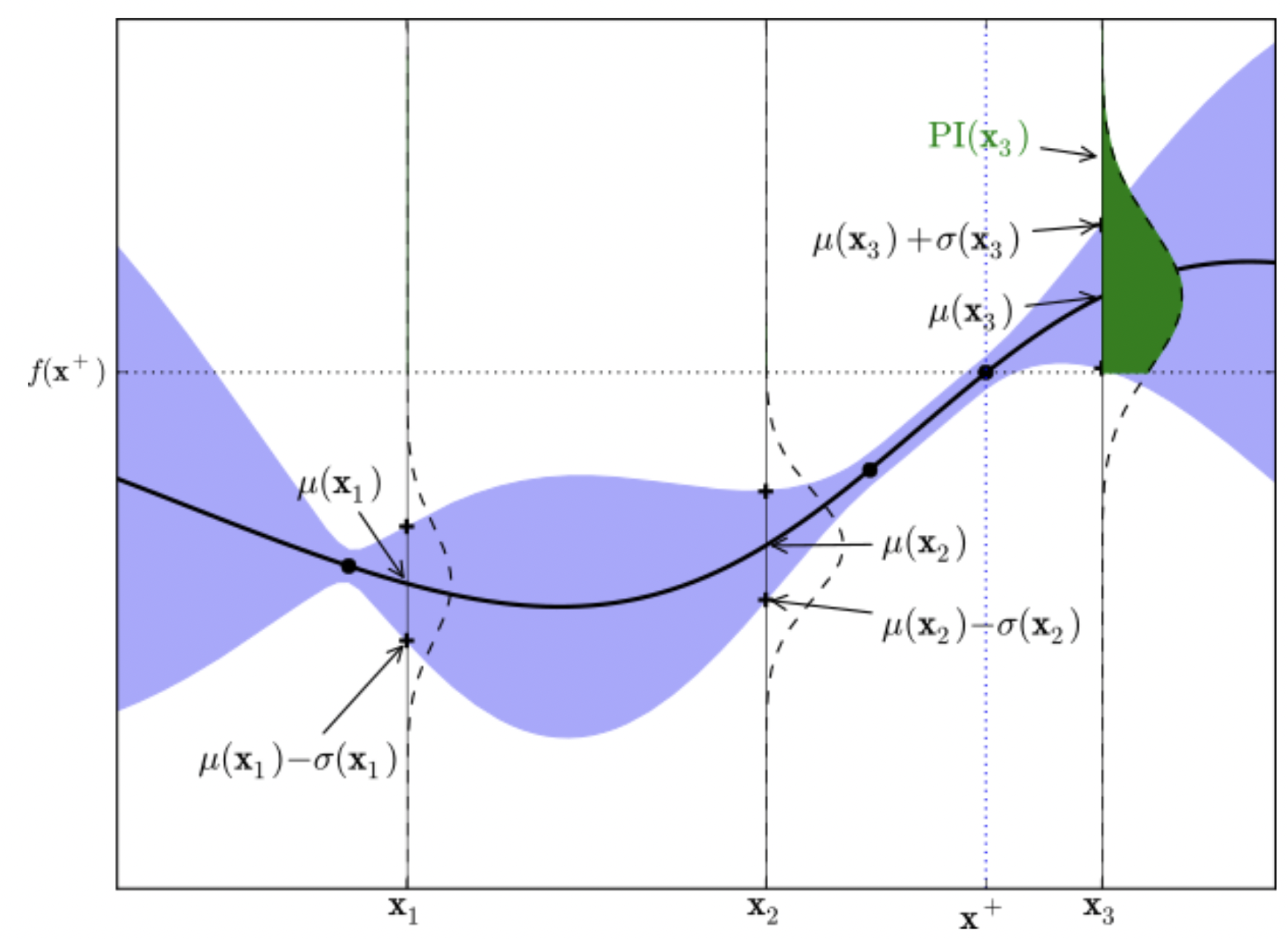
계속 설명하자면
1. 아까 샘플링한 10개에서 최고의 값을 구하고 best_mu로 저장한다.
2. 다음 탐색할 지점을 정하기 위해 한번 더 랜덤하게 10개를 뽑은 후 각각의 지점에 대해서 EI값을 구한다 = score_list
3. 구해진 score_list에서 가장 높게 나온 값을 다음 탐색지점으로 정함 = x_new . 실제로 func으로 predict
4. 결과를 저장한다. (X ,y 에 )
5. iter 돌면서 반복
best_mu = max(model.predict(X))
X_new = sampler(n)
score_list = EI(X_new, model , best_mu)
x_new = X_new[score_list.argmax()]
y_new = obj_func(x_new)
X = np.vstack([X,x_new])
y = np.append(y,y_new)
최종 코드는 다음과 같음.
def main(n, num_iter):
X = sampler(n)
y = np.apply_along_axis(obj_func , axis = 1 , arr = X)
for _ in range(num_iter):
model = GRR(kernel = RBF() + WhiteKernel() , random_state =2022).fit(X,y)
best_mu = max(model.predict(X))
X_new = sampler(n)
score_list = EI(X_new, model , best_mu)
x_new = X_new[score_list.argmax()]
y_new = obj_func(x_new)
X = np.vstack([X,x_new])
y = np.append(y,y_new)
print(X)
return X[y.argmax()] , y.max()'Data Science > Bayesian' 카테고리의 다른 글
| <Bayesian> MAB 톰슨 샘플링 (0) | 2022.12.03 |
|---|---|
| <Bayesian> Variational Inference ( Pyro) (0) | 2022.11.12 |
| <Bayesian> MCMC, pyro 로 모델링 (HMC) (0) | 2022.10.30 |
| <Bayesian> Bayesian Regression + Pyro 간단 정리. (0) | 2022.10.01 |



