내가 보려고 만든 블로그
<Bayesian> Bayesian Regression + Pyro 간단 정리. 본문
베이지안 프로그래밍을 지원해주는 파이썬 라이브러리로 대표적인게 PYMC3 가 있다. 하지만 비교적 최근에 uber에서 (uber아닐수도있음) 확률적 프로그래밍을 해주는 라이브러리 Pyro를 공개했다. 장점은 pytorch 기반으로 만들어져 있어 pymc에 비해 빠르다. 단점은 참고할만한 공부자료가 거의 없다... 그나마 공식문서가 잘되있긴한데 모르는게 여전히 많다. pyro 공식문서에서 예제로 베이지안리그레션을 바탕으로 pyro를 쓰는 방법을 설명하여 이참에 베이지안 리그레션과 pyro를 간단히 정리한다.
Bayesian Regression
베이지안 리그레션과 기존의 리그레션의 차이라고 한다면 기존 W_0 , W_1 등의 파라미터를 고정된 값이 아니라 확률변수로 본다는 점이 있을 것이다 .
사후분포를 P(W | D) 를 구함에 있어 베이즈 룰을 이용해 사후분포를 다음과 같이 분해하고 다음과 같이 두가지 가정이 들어가게 된다. ( w는 파라미터 , D는 관측값 , 즉 p(w)는 사전분포 , P(D | W)는 likelihood 임.

1. 첫번째 가정의 경우 뒤에서 조금 더 설명하겠지만 conjugacy를 위하여 필요한 가정이다. 각 w들이 N(0,S)의 정규분포임을 가정한다.
2. 두번째 가정의 경우 P(D|W)는 정규분포의 기존가정에 의하여 정규분포를 따르게 된다.

위에서 정의한 가정을 바탕으로 사후분포를 전개하면 다시 log( P (W | D ) ) 는 평균과 분산이 초록색 글씨를 따르는 정규분포의 형태로 바뀌게 된다. 즉 p(w)는 정규분포라는 가정이 p(w|D)의 정규분포를 만들어 냈으므로 선형회귀에서 정규분포는 conjugate prior이다.
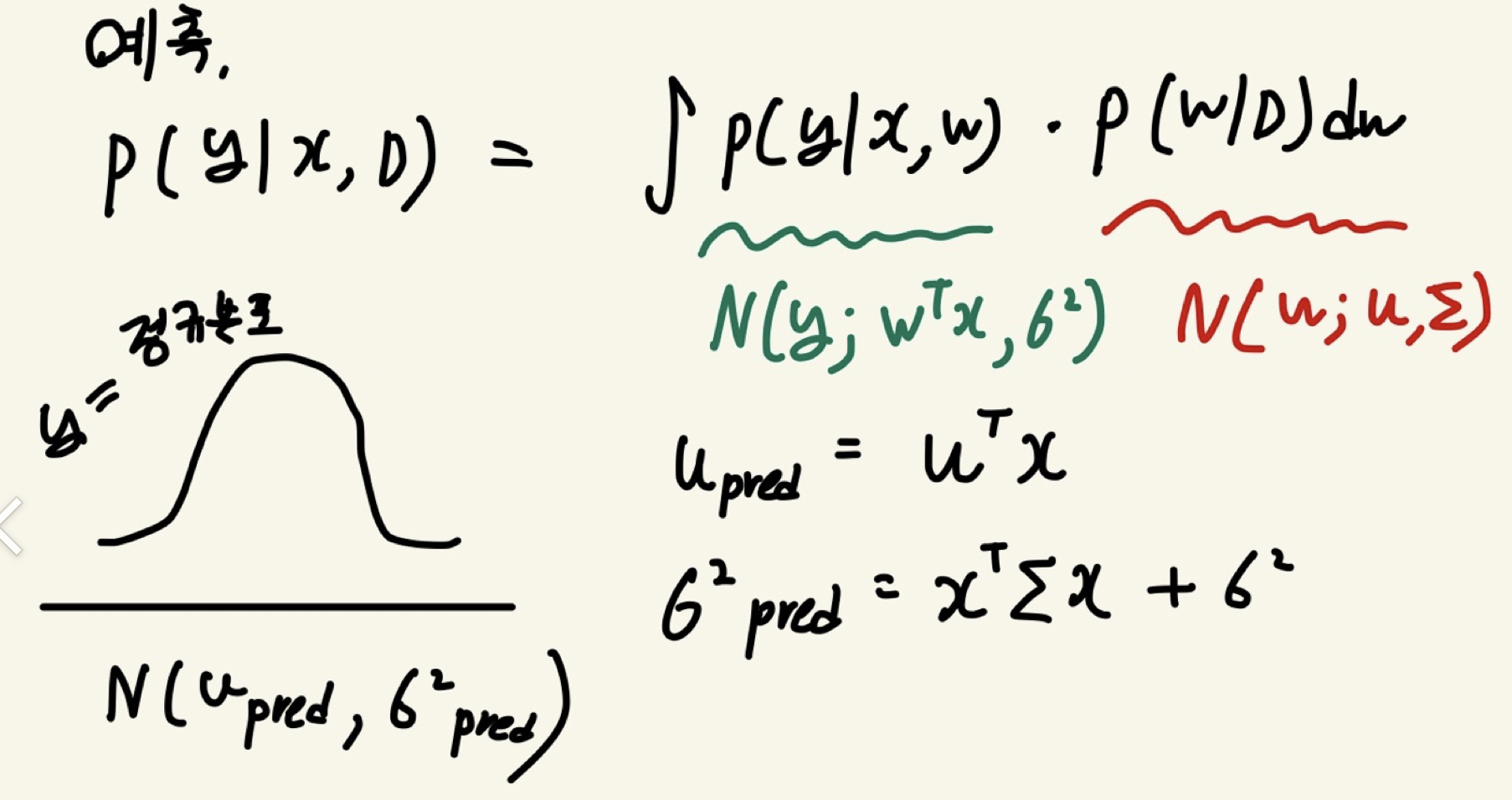
새로운 관측치 y ( 혹은 보통 x' 로 표기함) 에 대해 예측을 하면 p(y | x,w) * 사후분포 를 적분한 형태로 구해지는데 이를 다시 전개하면
y는 u_pred, 시그마_pred 를 따르는 정규분포로 구할 수 있다.
Pyro
pyro 공식문서의 아래 두 페이지를 참고하여 정리함. 하지만 모르는게 많음.. ㅠ
https://pyro.ai/examples/intro_long.html
Introduction to Pyro — Pyro Tutorials 1.8.2 documentation
Background: “guide” programs as flexible approximate posteriors In variational inference, we introduce a parameterized distribution \(q_{\phi}({\bf z})\) to approximate the true posterior, where \(\phi\) are known as the variational parameters. This di
pyro.ai
https://pyro.ai/examples/bayesian_regression.html
Bayesian Regression - Introduction (Part 1) — Pyro Tutorials 1.8.2 documentation
Optimizing the Evidence Lower Bound We will use stochastic variational inference (SVI) (for an introduction to SVI, see SVI Part I) for doing inference. Just like in the non-Bayesian linear regression model, each iteration of our training loop will take a
pyro.ai
베이지안 리그레션을 Pyro를 이용해 프로그래밍. 문서에서는 log(GDP) = mean 을 아프리카에 속하는지 여부 is_cont_africa 와 지형의 거친정도?? (ruggedness) 와 이 둘의 interaction term (is_conf_africa * ruggedness)을 이용해 표현함 . 다시 쓰면 다음과 같은 회귀모형을 베이지안 프로그래밍할 것이다.
mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness이를 Pyro의 모델로 표현하면 다음과 같다.
def model(is_cont_africa, ruggedness, log_gdp=None):
a = pyro.sample("a", dist.Normal(0., 10.))
b_a = pyro.sample("bA", dist.Normal(0., 1.))
b_r = pyro.sample("bR", dist.Normal(0., 1.))
b_ar = pyro.sample("bAR", dist.Normal(0., 1.))
sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness
with pyro.plate("data", len(ruggedness)):
return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)
pyro.render_model(model, model_args=(is_cont_africa, ruggedness, log_gdp), render_distributions=True)1. pyro.sample 하면 이름에서 알 수 있듯이 해당 분포에서 샘플링을 해준다. 각 w에 해당하는 a , b_a , b_r , b_ar을 정규분포에서 샘플링을 해준 모습. 베이지안 리그레션이기 때문에 위와같이 pyro.sample 을 사용하면 되겠고 만일 일반적인 linear regression 이라면 pyro.parameter 를 사용하면 된다 .( parameter는 고정된 모수 값 . )
2. pyro.plate 와 pyro.sampe(obs=log_gdp)
우선 with pyro.plate() 이 부분은 plate notation이라 하여 반복되는 변수들 혹은 샘플링한 변수 x_0, x_1 , .... x_n 등을 한번에 표현하기 위해 사용된다.
https://en.wikipedia.org/wiki/Plate_notation
Plate notation - Wikipedia
In Bayesian inference, plate notation is a method of representing variables that repeat in a graphical model. Instead of drawing each repeated variable individually, a plate or rectangle is used to group variables into a subgraph that repeat together, and
en.wikipedia.org
pyro.sample(obs= obs) 형식으로 넣주면 관측값을 샘플링값으로 사용하겠다는 뜻이다. 그래서 저 코드를 실행해보면 obs= log_gdp에 해당하는 값이 계속 반복적으로 나오는 것을 확인할 수 있다. 사후분포를 구할 때 사용되는 샘플값들을 넣주는 것.
pyro.render_model은 시각화 해주는 fuction이라 우선 패스.
다음으로 가이드 라는 것을 만들어 주어야 한다. Variational Inferecne를 통해 통해 사후분포를 추정할 때 사후분포를 근사하는 분포인 q를 가정하는 것을 봤을 것이다. 이 q를 만들어주는 과정이 가이드이다. 이 q를 추정하는 것은 pyro에서 자동으로 만들어주는 autoguide를 사용하거나 직접 custom guide를 만들 수 있다. 추가로 custom guide를 만들 때 주의 해야할 점은 pyro.sample 을 통해 확률변수를 만들어줄때 pyro.sample("변수이름 ", 분포) 와 같이 선언해야하는데 이 "변수이름" 이 모델에서 정의한 "변수이름" 과 1대1 맵핑되어야 한다.( 분포는 달라도 됨 근사분포이므로 ). 후에 vi에 대해 좀 더 자세히 서술할 예정.
auto_guide = pyro.infer.autoguide.AutoNormal(model)def custom_guide(is_cont_africa, ruggedness, log_gdp=None):
a_loc = pyro.param('a_loc', lambda: torch.tensor(0.))
a_scale = pyro.param('a_scale', lambda: torch.tensor(1.),
constraint=constraints.positive)
sigma_loc = pyro.param('sigma_loc', lambda: torch.tensor(1.),
constraint=constraints.positive)
weights_loc = pyro.param('weights_loc', lambda: torch.randn(3))
weights_scale = pyro.param('weights_scale', lambda: torch.ones(3),
constraint=constraints.positive)
a = pyro.sample("a", dist.Normal(a_loc, a_scale))
b_a = pyro.sample("bA", dist.Normal(weights_loc[0], weights_scale[0]))
b_r = pyro.sample("bR", dist.Normal(weights_loc[1], weights_scale[1]))
b_ar = pyro.sample("bAR", dist.Normal(weights_loc[2], weights_scale[2]))
sigma = pyro.sample("sigma", dist.Normal(sigma_loc, torch.tensor(0.05)))
return {"a": a, "b_a": b_a, "b_r": b_r, "b_ar": b_ar, "sigma": sigma}
마지막으로 optimizer를 adam으로 loss_function을 elbo로 그리고 사후분포를 추정함에 있어 vi 방법을 사용한다고 한다. 아래와 같이 코드를 작성해주면 된다.
adam = pyro.optim.Adam({"lr": 0.02}) # Consider decreasing learning rate.
elbo = pyro.infer.Trace_ELBO()
svi = pyro.infer.SVI(model, auto_guide, adam, elbo)마지막으로 트레인
%%time
pyro.clear_param_store()
# These should be reset each training loop.
auto_guide = pyro.infer.autoguide.AutoNormal(model)
adam = pyro.optim.Adam({"lr": 0.02}) # Consider decreasing learning rate.
elbo = pyro.infer.Trace_ELBO()
svi = pyro.infer.SVI(model, auto_guide, adam, elbo)
losses = []
for step in range(1000 if not smoke_test else 2): # Consider running for more steps.
loss = svi.step(is_cont_africa, ruggedness, log_gdp)
losses.append(loss)
if step % 100 == 0:
logging.info("Elbo loss: {}".format(loss))
plt.figure(figsize=(5, 2))
plt.plot(losses)
plt.xlabel("SVI step")
plt.ylabel("ELBO loss");'Data Science > Bayesian' 카테고리의 다른 글
| <Bayesian> MAB 톰슨 샘플링 (0) | 2022.12.03 |
|---|---|
| <Bayesian> Bayesian Optimization (0) | 2022.11.27 |
| <Bayesian> Variational Inference ( Pyro) (0) | 2022.11.12 |
| <Bayesian> MCMC, pyro 로 모델링 (HMC) (0) | 2022.10.30 |



